張皓 楊鋒平 張良 吳峰

中國石油集團工程材料研究院有限公司

 

摘要：為確定輸油氣管道異型B型套筒可修復缺陷的合理尺寸范圍，并確定B形套筒的最佳結構參數方案，采用有限元方法，針對Φ508 mm管道分析并建立了四種異型套筒構型，采用數值模擬方法驗證不同構型設計的適用性，并基于應力分析結果給出了異型B型套筒優選方案。結果表明直線導角型和橢圓曲線型異型套筒應力分布結果最優，考慮到加工精度及參數檢測難度，優先推薦直線導角型異型套筒工程應用。

關鍵詞：異型B型套筒；構型設計；應力分析

 

輸油氣管道作為長距離輸送原油和天然氣的專用設施，是全球能源基礎設施的重要組成部分，然而，管道在受到外載荷或腐蝕等影響時，可能形成服役安全隱患。在缺陷修復方面，目前國內外標準均規定其永久修復方式為B型套筒或換管。相比成本巨大的換管，B型套筒無疑是經濟性與安全性的首選[1]。SY/T 7666―2022《油氣管道缺陷修復用B型套筒》介紹，B型套筒修復技術是利用兩個由鋼板（或短節）制成的半圓柱外殼覆蓋在管道缺陷處，且待修復管道缺陷軸向長度中心位于套筒長度的二分之一位置，兩片套筒通過側焊縫焊接在一起，套筒端部采用角焊的方式焊接在輸送管道上。B型套筒的設計對其修復可靠性至關重要，套筒通常被設計成緊密地配合在管道的周圍，提供安全穩定的支撐結構[2]。對于外載荷引起的管道大變形缺陷，如管體屈曲及褶皺缺陷，異型B型套筒是一種行之有效的修復方法，然而其結構形式及相關參數確定方法目前鮮有研究分析。基于異形B型套筒的基本結構特征，本文設計了4種異型套筒構型，基于應力分析結果給出了異型B型套筒優選方案。

1  套筒構型設計

1.1  套筒設計基礎參數

為了修復管體屈曲、褶皺等大變形缺陷，異型B型套筒的基本結構為中間粗、兩端細的圓筒狀構型。根據變徑段曲線不同形式，異型B型套筒基于4種構型進行了參數化設計，研究中采用三個長度參數（600 mm、800 mm、1000 mm）和五個可修復缺陷高度參數（5 mm、10 mm、15 mm、20 mm、37 mm）來分析均勻載荷下的應力分布。分析采用的被修復管道外徑為508 mm。

變徑段的曲線設計是本文研究的重點之一，根據曲線表達函數的不同，研究中將變徑段分為一次曲線型、二次曲線型和高次曲線型。基于該思路，本研究設計了4種異型套筒構型：直線導角型、橢圓曲線型、拋物線型和Sigmond曲線型。以直線導角型異型套筒為例，套筒的截面形狀被定義為幾個不同的元素，即：直線段L1和L2；圓弧段R1和R2。每種異型套筒構型及關鍵尺寸等的詳細說明見圖 1～圖 4。

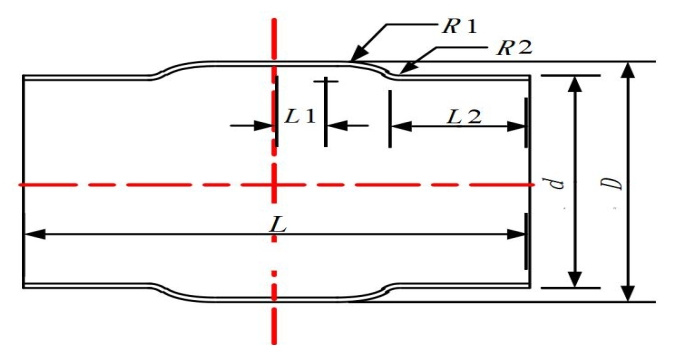
圖 1 直線導角型套筒結構

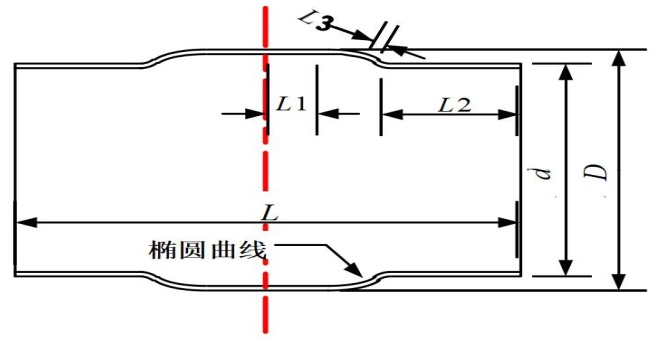
圖 2 橢圓曲線型套筒結構

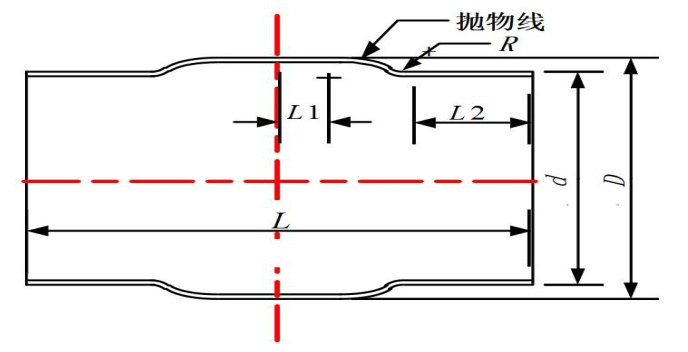
圖 3 拋物線導角型套筒結構

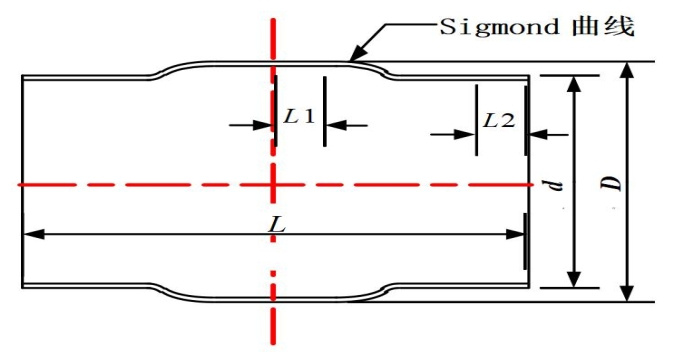
圖 4 Sigmond曲線型套筒結構

圖中根據套筒構型的不同分別設置一個初始的優化參數，即指定大徑段、小徑段的長度和各導角的半徑。初始值的設置不影響最終的優化結果。

在獲得4種套筒結構形式后，使用參數化建模工具Cero3.0軟件生成四種不同套筒構型的分析模型，以便對這些模型進行有限元分析。計算及分析目的是優化各構型B型套筒的關鍵參數，最大限度地減少應力集中。

1.2  有限元模型

以直線導角型B型套筒為例，為了避免異形套筒的端部效應，套筒端部的長度延長到2.5 m。邊界條件為遠端兩端面固結，管道及套筒內壓載荷條件為8 MPa法向均壓。結構評估以L長度上的應力集中水平為優化對象。以直線導角型B型套筒為例，優化前設置的初始尺寸如表 1所示。

表 1 直線導角型B型套筒優化初始參數

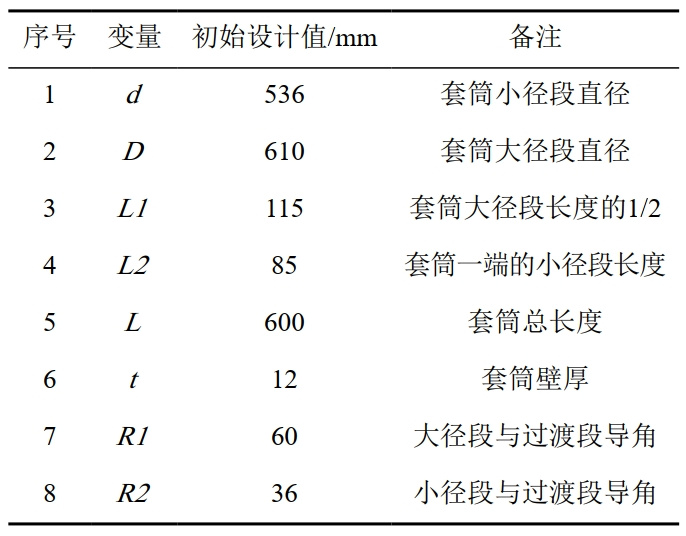
1.3  優化目標

本文的主要目標是找到滿足以下條件的最佳套筒輪廓及其結構尺寸，計算中應滿足以下條件：

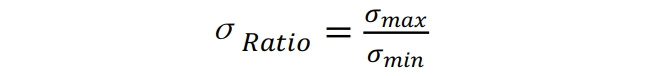
應力集中系數小于2；異形B型套筒的最大應力小于屈服強度的72%。

對于套筒的應力集中優化，選擇四個目標函數，即：σRatio為應力集中系數=最大應力與最小應力之比；σmax為套筒段最大VonMises應力；σavg為套筒段的平均VonMises應力；σmin為套筒段最小VonMises應力。

2  應力計算與結果分析

2.1  設計空間

以直線導角型B型套筒為例，存在四個設計變量（L1、L2、R1、R2），每個變量取4個因子的初始設置值，以形成設計空間。本研究中涉及的異形B型套筒結構的設計考慮了各種因素對計算結果的影響，包括大徑段長度L1、大徑段與變徑段導角R1、小徑段長度L2和小徑段與變徑段導角R2。計算中采用控制變量法和正交實驗法來減少模擬次數，通過對單個因素的模擬和數學模型的建立，研究了不同因素的影響規律，進而綜合分析了多因素的影響，建立了統一的影響面和參數影響水平相關矩陣。利用不同參數組合的仿真結果對預測模型進行驗證和改進，確保優化模型的可靠性。

在優化計算過程中，目標函數收斂誤差小于0.1%。采樣點選擇使用中心復合設計方法，其中采樣點由中心點、輸入變量軸的端點和水平因子點組成。通過這種方法形成的部分因子樣本點的數量隨著設計變量的增加而增加，根據N=1+2n+（2n-f）計算（其中f是部分因子的數量，n是輸入參數的數量，N是形成的樣本點的數目）。總共需要計算25個模型。

根據相關修復標準中的推薦尺寸條件，其約束條件為：L1>110、L2>80、R1>60、R2>36。此外，空間幾何圖形約束的限制如下：

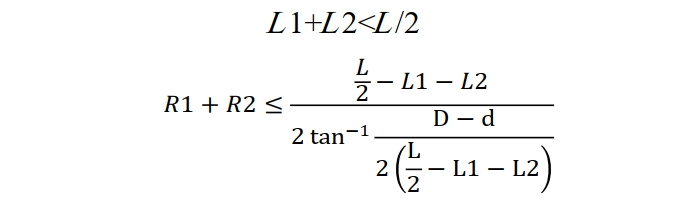
2.2  不同缺陷高度和套筒長度的異型套筒優化結果

經有限元計算分析，得出了各構型套筒的優化后參數。限于篇幅，本文給出了直線導角型和Sigmond曲線型的最終優化結果。

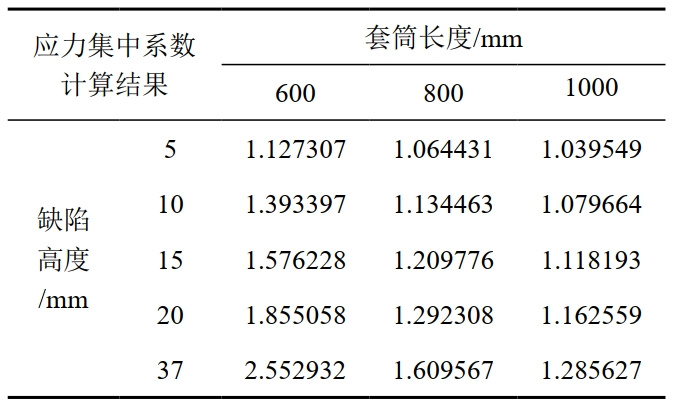
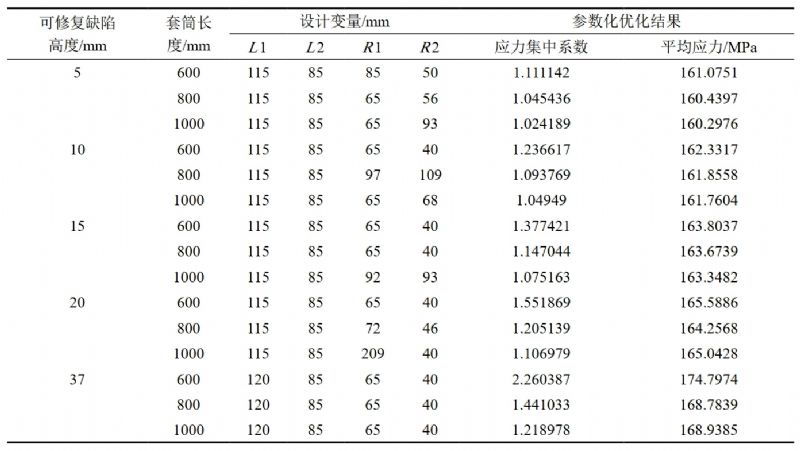
直線導角型套筒優化結果見表 2，優化結果表明，缺陷高度越大，應力集中系數越大，套筒應力儲備裕度越小。表 3所示的計算結果表明，異型套筒可修復缺陷高度越大，套筒長度越小，應力集中系數越大，相應的套筒應力儲備裕度越小。

表 2 直線導角型套筒優化結果

表 3 直線導角型套筒應力集中系數優化結果

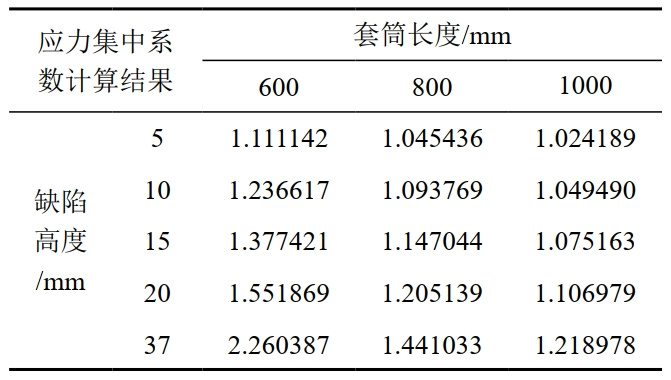
圖 5說明了缺陷高度與套筒應力集中系數之間的關系。圖中x軸表示以毫米為單位的缺陷高度，而y軸表示套筒應力集中系數。相同參數水平下的套筒應力分布結果比較表明，缺陷高度與套筒應力集中因子呈正相關，套筒長度與套筒應力集中因子負相關。此外，缺陷高度與套筒的最大VonMises應力呈正相關，而套筒長度則呈負相關。當缺陷高度保持不變時，較大的套筒長度下套筒應力集中系數較小，相應的應力儲備裕度越大，反之亦然。

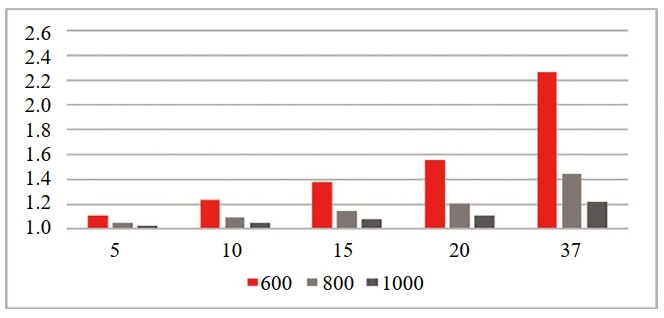
圖 5 直線導角型套筒尺寸參數對應力集中系數的影響

Sigmond曲線型套筒優化結果，其結構尺寸根據相關修復標準中推薦的尺寸條件及其約束條件，確定設計變量L1>110、L2>80。此外，空間幾何圖形約束的限制如下：

L1+L2<L/2

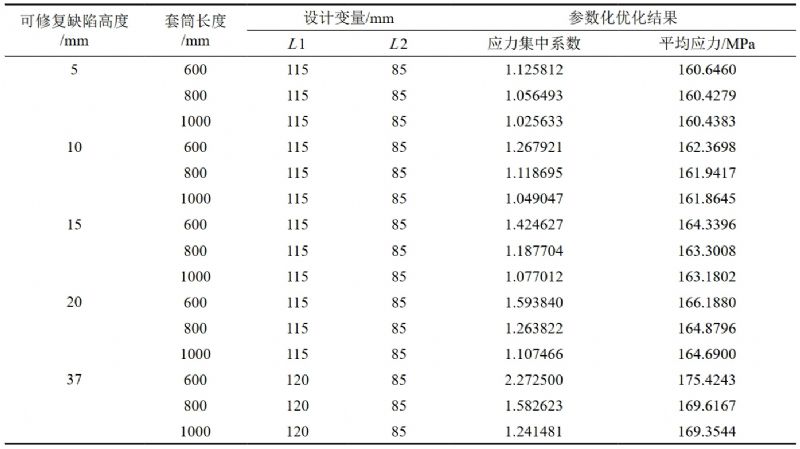
最終優化結果匯編見表 4。

表 4 Sigmond曲線型套筒優化結果（套筒長度 L=600 mm）

計算結果與直線導角型套筒類似，即缺陷高度越大，應力集中系數越大，套筒應力儲備裕度越小。表 5所示的計算結果表明，Sigmond曲線型套筒可修復缺陷高度越大，套筒長度越小，應力集中系數越大，相應的套筒應力儲備裕度越小。

表 5 Sigmond曲線型套筒應力集中系數優化結果

此外，圖 6中所示的計算結果表明，應力集中因子隨著缺陷高度的增加而增大，而隨著套筒長度的增加而減小。此外，套筒的最大VonMises應力與缺陷高度呈正相關，與套筒長度負相關。

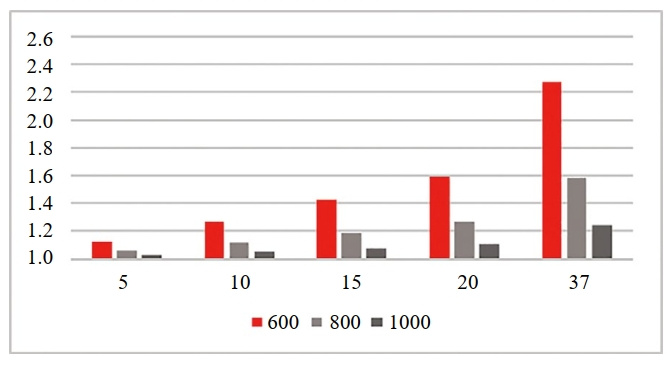
圖 6 Sigmond曲線型套筒尺寸參數對應力集中系數的影響

綜上，缺陷高度和套筒長度在決定套筒的應力集中系數、套筒應力儲備裕度和最大VonMises應力方面起著重要作用。這項研究的結果表明了關鍵設計參數對異形套筒性能的影響，并為該類異型套筒選擇合適的結構和可修復缺陷尺寸參數方案提供參考。

2.3  不同構型異型B型套筒優化結果

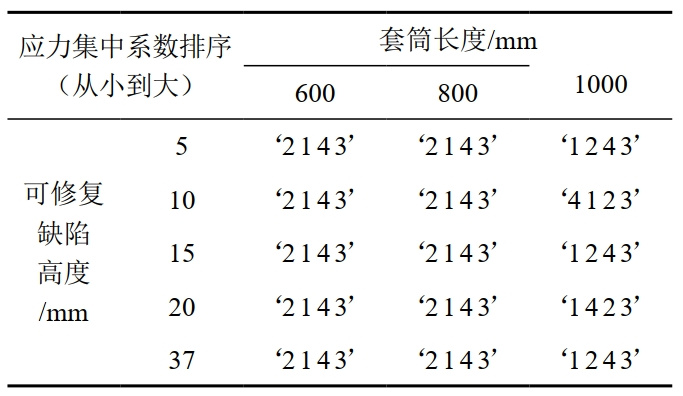
表 6中，1表示直線導角型套筒，2表示橢圓曲線型套筒，3表示拋物線導角型套筒，4表示Sigmond曲線型套筒。計算結果表明，當套筒長度為600/800mm時，橢圓曲線型應力集中因子最小，而當套筒長度為1000 mm時，直線導角型套筒應力集中因子最小。此外，橢圓曲線型在套筒長度為600/800 mm計算得到的最大應力值最小，而當套筒長度為1000 mm時，直線導角型/Sigmond曲線型套筒計算得到的最大應力值最小。

表 6 不同構型異型套筒優化結果及優選方案

3  結論

（1）基于變徑段曲線不同形式，設計了4種不同構型的異型B型套筒，分別為直線導角型、橢圓曲線型、拋物線導角型和Sigmond曲線型。

（2）采用全參數化建模方法開展了各構型的異型套筒有限元計算，采用多目標遺傳優化方法，對具有特定缺陷高度和套筒長度的異型B形套筒的設計變量參數進行了初始設置和邊界條件限制，得到了合適的結構尺寸組合，以便提高計算效率并選出最優構型。

（3）設計了一系列可修復缺陷高度和套筒長度以進行對比分析，每種構型的異型套筒均計算了5種缺陷高度和3個套筒長度下的應力分布。結果表明，當套筒長度為600/800 mm時，橢圓曲線型套筒應力分布結果最優；當套筒長度為1000 mm時，直線導角型套筒應力分布結果最優。

（4）從工程應用方面考慮，建議異型套筒加工時優先選用直線導角型套筒，加工難度相對較小，且關鍵尺寸更易控制和檢測；可將橢圓曲線型套筒作為備選方案，待加工及測量條件允許時再行應用。

 

參考文獻：

[1]Wang, Y., Zhang, Y., Zhang, J., & Li, X. A study of the mechanical behavior of B-type sleeves for oil pipelines. Journal of Petroleum Science and Engineering, 145, 20-28. 2016.

[2]Li, X., Wang, Y., Zhang, Y., & Zhang, J. A review of B-type sleeves for oil pipelines. Journal of Pipeline Engineering, 17(1), 1-10. 2018.

作者簡介：張皓，1990年生，畢業于西安交通大學航天學院，高級工程師，現從事油氣輸送管道及站場設備安全評價及失效分析研究。聯系方式：15829616623，zhanghao6@cnpc.com.cn。